From Serial to Supercomputer: Scaling Fourier Transforms with MPI and ARCHER2

Introduction

In the realm of computational science, solving complex mathematical problems often demands significant computational power and time¹. The Fourier Transform (FT) is one such algorithm that is widely used in various fields such as signal processing, image analysis, and data compression. However, FT computations can become exceedingly resource-intensive, especially for large problem sizes. To address these challenges, parallel computing techniques are employed to enhance computational efficiency and reduce execution time.

This article aims to explore two foundational concepts in parallel computing: Amdahl’s Law and Gustafson’s Law. Amdahl’s Law provides insight into the potential speedup of a parallelised task, highlighting the limits imposed by the serial portion of the computation². Conversely, Gustafson’s Law offers a perspective on scaling performance by considering the workload that can be managed within a given time when more processors are added³. Understanding these laws is crucial for optimising parallel applications and effectively utilising computational resources.

To illustrate these concepts, we will use a real-world example involving the Fourier Transform (FT). We will start by implementing the FT algorithm in a serial manner, followed by its parallelisation using the Message Passing Interface (MPI). The performance of both implementations will be analysed and compared using strong and weak scaling principles. Finally, we will deploy the parallelised code on the ARCHER2 supercomputer⁴ and use the SLURM job scheduler⁵ to conduct performance tests, demonstrating the real-world application of these concepts.

By exploring these scaling laws through a practical FT example, this article aims to provide a comprehensive understanding of parallel computing’s theoretical and practical aspects. This knowledge is not only relevant to FT computations but also extends to various scientific and engineering disciplines. Large-scale simulations are a crucial part of the research and development process, making it a valuable resource for professionals in these fields.

Theoretical Background

Amdahl’s Law

Amdahl’s Law, formulated by Gene Amdahl in 1967, defines the theoretical maximum speedup of a task that can be achieved through parallelisation. It highlights the impact of the serial portion of a computation on overall performance gains.

Amdahl’s Law is mathematically expressed as: $S = \frac{1}{(1 - P) + \frac{P}{N}}$

where:

• $S$ is the speedup of the program.
• $P$ is the proportion of the program that can be parallelised.
• $N$ is the number of processors.

The law indicates that as the number of processors $N$ increases, the speedup $S$ approaches a limit determined by the program’s serial fraction $1 - P$. This implies that even with an infinite number of processors, the maximum speedup is constrained by the non-parallelisable portion of the computation.

Strong Scaling

Strong scaling refers to the scenario where the problem size remains constant while the number of processors increases. The goal is to reduce the computation time by distributing the workload across more processors. Amdahl’s Law is particularly relevant in this context, as it helps understand the diminishing returns of adding more processors.

The efficiency of strong scaling can be evaluated using the equation: $\text{efficiency} = \frac{S}{N}$

Gustafson’s Law

Gustafson’s Law, proposed by John L. Gustafson in 1988, offers a different perspective on parallel computing by focusing on the scalability of the problem size with the number of processors. Instead of keeping the problem size constant, Gustafson’s Law considers increasing the problem size proportionally with the number of processors.

Gustafson’s Law is expressed as: $S(N) = N - (1 - P) \cdot (N - 1)$

where:

• $S(N)$ is the scaled speedup.
• $P$ is the parallel fraction of the program.
• $N$ is the number of processors.

This law suggests that as the number of processors increases, larger problems can be solved in the same amount of time, thus providing a more optimistic view of parallel computing scalability.

Weak Scaling

Weak scaling is concerned with maintaining a constant workload per processor as the number of processors increases. This approach aims to keep the execution time constant while solving larger problems with more processors. Gustafson’s Law is particularly useful in understanding weak scaling, as it emphasises the benefits of parallel computing when the problem size scales with the number of processors.

Fourier Transform

The Fourier Transform (FT) is a mathematical operation that transforms a function of time (or space) into a function of frequency. It is widely used in signal processing, image analysis, and many other fields. The Discrete Fourier Transform (DFT) is used in practical applications and is defined as:

$X_k = \sum_{n=0}^{N-1} x_n e^{-i 2 \pi k n / N}$

where:

• $X_k$ is the DFT of the sequence $x_n$.
• $N$ is the number of samples.

The Fast Fourier Transform (FFT) is an algorithm that efficiently computes the DFT, reducing the computational complexity from $\mathcal{O}(N^2)$ to $\mathcal{O}(N \log N)$. The computational complexity of the FFT algorithm is $\mathcal{O}(N \log N)$, which significantly improves performance over the naive DFT approach. However, for very large datasets or high-dimensional transforms, even this improved complexity can lead to substantial computation times, necessitating further optimisation through parallelisation.

Serial Implementation

Outline of the Serial Algorithm for Solving the DFT Problem

The Discrete Fourier Transform (DFT) is a mathematical technique used to transform a sequence of complex numbers into another sequence of complex numbers, representing the frequency domain of the original sequence. The Fast Fourier Transform (FFT) is an efficient algorithm for computing the DFT. The serial implementation of the DFT involves the following steps:

1. Initialisation:

   • Allocate memory for the input, forward transform, inverse transform, and twiddle factors.
   • Populate the input array with sample data.
   • Precompute the twiddle factors (complex exponentials) required for the FT for each dimension.

2. Fourier Transform Computation:

   • Apply the FT algorithm to transform the input data from the time domain to the frequency domain.
   • Apply the inverse FT algorithm to transform the data back from the frequency domain to the time domain, verifying the correctness of the forward transform.

3. Performance Metrics:

   • Measure and print the time taken for precomputation, forward transform, and inverse transform.

4. Cleanup:

   • Free the allocated memory for the input, twiddles, forward, and inverse arrays.

Code Snippets and Implementation

The following code snippets provide a comprehensive implementation of the FT in a serial manner. The code is organised into several files, each serving a distinct purpose in the overall algorithm. Here is a brief description of what each file does:

• serial.c: This is the main file that initialises the data structures, precomputes twiddle factors, performs the Fourier Transform, and measures the execution time. It handles both the forward and inverse transforms and ensures that the allocated memory is freed correctly after use.
• fourier_transform.c: This file contains the core FT functions. It includes functions to run the transform, precompute twiddle factors, and the main FT computation across three dimensions. The transform_index function is used to compute the FT for a specific index.
• utils.c: This file provides utility functions to create and manage 3D arrays, generate sample data, and print a subset of the array values for verification purposes. These utilities simplify memory management and data initialisation.
• arralloc.c: This file includes functions to dynamically allocate memory for multidimensional arrays. It ensures that the memory is properly aligned and sets up the necessary pointers to form dope-vector arrays, facilitating efficient access and manipulation of the array elements.

Here are the complete code listings for each file:

serial.c

#include <stdio.h>
#include <complex.h>
#include <time.h>
#include <stddef.h>
#include "fourier_transform.h"
#include "utils.h"

int main(int argc, char *argv[]) {
    int l = 48, m = 48, n = 48;
    double complex ***input = NULL;
    double complex ***twiddles = NULL;
    double complex ***forward = NULL;
    double complex ***inverse = NULL;
    clock_t start, stop, duration;

    // initialisation
    // allocate memory for the 3d input array
    input = create_sample_data(l, m, n);
    if (input == NULL) {
        fprintf(stderr, "error: unable to allocate memory for the 'input' array.\n");
        return 1;
    }

    // time and precompute one-dimensional twiddle factors for each dimension
    start = clock();
    twiddles = precompute_twiddles(l, m, n);
    stop = clock();
    if (twiddles == NULL) {
        fprintf(stderr, "error: unable to allocate memory for the 'twiddles' array.\n");
        free_3d_array(input);
        return 1;
    }

    // allocate memory for the 3d forward and inverse array
    forward = create_3d_array(l, m, n);
    inverse = create_3d_array(l, m, n);
    if (forward == NULL || inverse == NULL) {
        fprintf(stderr, "error: unable to allocate memory for the 'forward' or 'inverse' array.\n");
        free_3d_array(input);
        free_3d_array(twiddles);
        free_3d_array(forward);
        free_3d_array(inverse);
        return 1;
    }

    printf("running fourier transform on %dx%dx%d problem using %d process(es).\n", l, m, n, 1);
    printf("time taken to precompute twiddles: %f seconds.\n", (double) (stop - start) / CLOCKS_PER_SEC);
    printf("a small part of the input array 'input':\n");
    print_numbers(input, 3);

    // run the fourier transform forward and inverse, checking correctness
    // perform forward transform
    duration = run_transform(input, forward, l, m, n, 0, twiddles);
    printf("execution time (forward): %f seconds.\n", (double) duration / CLOCKS_PER_SEC);
    printf("a small part of the output array 'forward':\n");
    print_numbers(forward, 3);

    // perform inverse transform
    duration = run_transform(forward, inverse, l, m, n, 1, twiddles);
    printf("execution time (inverse): %f seconds.\n", (double) duration / CLOCKS_PER_SEC);
    printf("a small part of the output array 'inverse':\n");
    print_numbers(inverse, 3);

    // check how close 'inverse' is to 'input'
    double error = check_inverse_error(input, inverse, l, m, n);
    printf("relative error after inverse = %e\n", error);

    // free allocated memory
    free_3d_array(input);
    free_3d_array(twiddles);
    free_3d_array(forward);
    free_3d_array(inverse);

    return 0;
}

fourier_transform.c

#include <math.h>
#include <complex.h>
#include <time.h>
#include <stddef.h>
#include "arralloc.h"
#include "fourier_transform.h"

clock_t run_transform(double complex ***input, double complex ***output, int l, int m, int n, int inverse, double complex ***twiddles) {
    clock_t start = clock();
    fourier_transform(input, output, l, m, n, inverse, twiddles);
    clock_t duration = clock() - start;

    return duration;
}

double complex ***precompute_twiddles(int l, int m, int n) {
    double complex ***twiddles = (double complex ***) arralloc(sizeof(double complex), 3, 3, l > m ? l : m, l > n ? l : n);
    if (twiddles == NULL) {
        return NULL;
    }

    for (int d = 0; d < 3; d++) {
        int length = (d == 0) ? l : (d == 1) ? m : n;
        for (int i = 0; i < length; i++) {
            for (int j = 0; j < length; j++) {
                double factor = -2 * M_PI * i * j / length;
                twiddles[d][i][j] = cexp(I * factor);
            }
        }
    }

    return twiddles;
}

void fourier_transform(double complex ***input, double complex ***tilde, int l, int m, int n, int inverse, double complex ***twiddles) {
    double total = (double) (l * m * n);
    for (int u = 0; u < l; u++) {
        for (int v = 0; v < m; v++) {
            transform_index(input, tilde[u][v], l, m, n, u, v, total, inverse, twiddles);
        }
    }
}

void transform_index(double complex ***input, double complex *slice, int l, int m, int n, int u, int v, double total, int inverse, double complex ***twiddles) {
    for (int w = 0; w < n; w++) {
        double complex sum = 0.0 + I * 0.0;
        for (int x = 0; x < l; x++) {
            // twiddle in dimension 0: twiddles[0][u][x]
            double complex factor_ux = inverse ? conj(twiddles[0][u][x]) : twiddles[0][u][x];

            for (int y = 0; y < m; y++) {
                // twiddle in dimension 1: twiddles[1][v][y]
                double complex factor_uy = inverse ? conj(twiddles[1][v][y]) : twiddles[1][v][y];

                for (int z = 0; z < n; z++) {
                    // twiddle in dimension 2: twiddles[2][w][z]
                    double complex factor_uz = inverse ? conj(twiddles[2][w][z]) : twiddles[2][w][z];
                    double complex product = input[x][y][z] * factor_ux * factor_uy * factor_uz;

                    sum += product;
                }
            }
        }

        if (inverse) {
            sum /= total; // ensure normalisation
        }
        slice[w] = sum;
    }
}

utils.c

#include <stdio.h>
#include <stdlib.h>
#include <complex.h>
#include <math.h>
#include "utils.h"
#include "arralloc.h"

double complex ***create_3d_array(int l, int m, int n) {
    return (double complex ***) arralloc(sizeof(double complex), 3, l, m, n);
}

void free_3d_array(double complex ***array) {
    free(array);
}

double complex ***create_sample_data(int l, int m, int n) {
    double complex ***input = create_3d_array(l, m, n);
    if (!input) return NULL;

    for (int i = 0; i < l; i++) {
        for (int j = 0; j < m; j++) {
            for (int k = 0; k < n; k++) {
                input[i][j][k] = (i * 10 + j * 5 + k * 2) + I * (i * 10 - j * 5 - k * 2);
            }
        }
    }
    return input;
}

void print_numbers(double complex ***input, int count) {
    for (int u = 0; u < 1; u++) {
        for (int v = 0; v < 1; v++) {
            for (int w = 1; w <= count; w++) {
                printf("%g + %gi\n", creal(input[u][v][w]), cimag(input[u][v][w]));
            }
        }
    }
    printf("\n");
}

double check_inverse_error(double complex ***original, double complex ***inverted, int l, int m, int n) {
    double norm_diff = 0.0, norm_orig = 0.0;
    for (int i = 0; i < l; i++) {
        for (int j = 0; j < m; j++) {
            for (int k = 0; k < n; k++) {
                double complex difference = original[i][j][k] - inverted[i][j][k];
                norm_diff += creal(difference) * creal(difference) + cimag(difference) * cimag(difference);

                double complex value = original[i][j][k];
                norm_orig += creal(value) * creal(value) + cimag(value) * cimag(value);
            }
        }
    }
    return sqrt(norm_diff / norm_orig);
}

arralloc.c

#include <stdint.h>
#include <stdlib.h>
#include <stdarg.h>
#include "arralloc.h"

// function to align the address
void *align(void *address, size_t alignment) {
    return (void *) (((uintptr_t) address + alignment - 1) & ~(alignment - 1));
}

// allocate a pseudo array of any dimensionality and type with specified size for each dimension.
void *arralloc(size_t size, int number_of_dimensions, ...) {
    va_list arguments;
    void **pointer, **start;
    int dimension_index;
    long number_of_pointers = 0, number_of_data = 1;
    int *dimensions;
    // setting alignment size to 32
    size_t alignment_size = 32;

    va_start(arguments, number_of_dimensions);

    // code only works for 'word' objects
    if (size % sizeof(int) != 0) {
        va_end(arguments);
        return NULL;
    }

    // align on both size and alignment_size
    while ((alignment_size % size) != 0) {
        alignment_size++;
    }

    // allocate space for dimension sizes
    dimensions = (int *) malloc(number_of_dimensions * sizeof(int));
    if (dimensions == NULL) {
        va_end(arguments);
        return NULL;
    }

    // accumulate number of pointers & data items
    for (dimension_index = 0; dimension_index < number_of_dimensions; dimension_index++) {
        dimensions[dimension_index] = va_arg(arguments, int);
        number_of_data *= dimensions[dimension_index];
        if (dimension_index < number_of_dimensions - 1) {
            number_of_pointers += number_of_data;
        }
    }
    va_end(arguments);

    // allocate space for pointers and data
    start = (void **) malloc((size_t) ((number_of_data * size) + alignment_size + (number_of_pointers * sizeof(void **))));
    if (start == NULL) {
        free(dimensions);
        return NULL;
    }

    // set up pointers to form dope-vector array
    setup_subarray(alignment_size, size, number_of_dimensions - 1, 1, &pointer, start, dimensions, 0);
    free(dimensions);

    return (void *) pointer;
}

// helper function to set up subarrays
void setup_subarray(size_t alignment_size, size_t size, int number_of_dimensions, int previous_dimension, void ***previous_pointer, void **current_pointer, int *dimensions, int index) {
    // aligned pointer only used in last recursion
    int *aligned_pointer = (int *) align(current_pointer, alignment_size);
    int **previous_pointer_cast = (int **) previous_pointer;
    int i, dimension = dimensions[index];

    // general case - set up pointers to pointers
    if (number_of_dimensions > 0) {
        for (i = 0; i < previous_dimension; i++) {
            // previous level points to us
            previous_pointer[i] = current_pointer + i * dimension;
        }
        setup_subarray(alignment_size, size, number_of_dimensions - 1, previous_dimension * dimension, (void ***) current_pointer, current_pointer + previous_dimension * dimension, dimensions, (index + 1));
    } else {
        // last recursion - set up pointers to data
        for (i = 0; i < previous_dimension; i++) {
            previous_pointer_cast[i] = aligned_pointer + (i * dimension) * size / sizeof(int);
        }
    }
}

This collection of files provides a complete implementation of the FT in a serial manner. Each file has a specific role, from initialising and managing data structures to performing the core FT computations and handling utility functions for memory management and data manipulation. By organising the code this way, we achieve modularity and ease of maintenance, allowing for efficient debugging and potential future enhancements.

Performance Metrics for the Serial Implementation

The following performance metrics were recorded during the execution of the FT on a $48 \times 48 \times 48$ problem using a single process:

• Time taken to precompute twiddles: 0.000325 seconds
• Execution time (forward transform): 101.249645 seconds
• Execution time (inverse transform): 111.477108 seconds

These metrics indicate the time required to compute the twiddle factors and the time to perform the forward and inverse Fourier Transforms on the given dataset. The input and output data snippets briefly examine the transformation results.

Sample output snippets:

• Input array:

  2 + -2i
  4 + -4i
  6 + -6i

• Forward transform output:

  1.57672e+06 + 1.7979e+06i
  729438 + 950622i
  445392 + 666576i

• Inverse transform output:

  2 + -2i
  4 + -4i
  6 + -6i

These results demonstrate the accuracy of the FT, as the inverse transform returns the original input values. Furthermore, these metrics indicate the time complexity of the serial implementation and provide a baseline for comparing the performance improvements achieved through parallelisation.

Parallel Implementation with MPI

Introduction to MPI (Message Passing Interface)

The Message Passing Interface (MPI) is a standardised and portable message-passing system designed to facilitate parallel computing⁶. MPI enables processes to communicate with each other by sending and receiving messages, which allows for the coordination and synchronisation necessary for parallel execution. MPI is widely used in high-performance computing (HPC) applications due to its scalability and efficiency. For a more detailed introduction to MPI, please see our previous article, ”Introduction to Parallel Programming with MPI”⁷.

Code Snippets and Implementation

Two new files were added to parallelise the serial FT code using MPI: parallel.c and parallel_fourier_transform.c. The primary modifications involve initialising MPI, distributing the workload among processes, and using MPI functions for communication and synchronisation:

• parallel.c: This is the main file that initialises MPI, allocates memory for arrays, performs the Fourier Transform in parallel, and ensures proper cleanup.
• parallel_fourier_transform.c: This file contains the core parallel FT functions and handles the communication between processes.

Here are the full code listings:

parallel.c

#include <mpi.h>
#include <stdio.h>
#include <stdlib.h>
#include <complex.h>
#include <time.h>
#include <getopt.h>
#include "parallel_fourier_transform.h"
#include "fourier_transform.h"
#include "utils.h"

void print_usage(char *program_name) {
    printf("usage: %s [-l <value>] [-m <value>] [-n <value>] [-h]\n", program_name);
    printf("   or: %s -a <value>\n", program_name);
    printf("options:\n");
    printf("  -l <value>   set the value of l\n");
    printf("  -m <value>   set the value of m\n");
    printf("  -n <value>   set the value of n\n");
    printf("  -a <value>   set the value of l, m, and n to the same value\n");
    printf("  -h           display this help message\n");
}

int main(int argc, char *argv[]) {
    int l = 48, m = 48, n = 48;
    int option;

    while ((option = getopt(argc, argv, "l:m:n:a:h")) != -1) {
        switch (option) {
            case 'l':
                l = atoi(optarg);
                break;
            case 'm':
                m = atoi(optarg);
                break;
            case 'n':
                n = atoi(optarg);
                break;
            case 'a':
                l = m = n = atoi(optarg);
                break;
            case 'h':
                print_usage(argv[0]);
                return 0;
            default:
                print_usage(argv[0]);
                return 1;
        }
    }

    int rank, size;
    MPI_Init(&argc, &argv);
    MPI_Comm_rank(MPI_COMM_WORLD, &rank);
    MPI_Comm_size(MPI_COMM_WORLD, &size);

    double complex ***input = NULL;
    double complex ***twiddles = NULL;
    double complex ***forward = NULL;
    double complex ***inverse = NULL;
    double start, stop, duration;

    // check if l is cleanly divisible by the number of processes
    if (l % size != 0) {
        if (rank == 0) {
            fprintf(stderr, "error: the value of l (%d) is not cleanly divisible by the number of processes (%d).\n", l, size);
        }
        MPI_Finalize();
        return 1;
    }

    // initialisation
    // allocate memory for the 3d input array
    input = create_sample_data(l, m, n);
    if (input == NULL) {
        fprintf(stderr, "error: unable to allocate memory for the 'input' array.\n");
        MPI_Finalize();
        return 1;
    }

    // time and precompute one-dimensional twiddle factors for each dimension
    start = MPI_Wtime();
    twiddles = precompute_twiddles(l, m, n);
    stop = MPI_Wtime();
    if (twiddles == NULL) {
        fprintf(stderr, "error: unable to allocate memory for the 'twiddles' array.\n");
        free_3d_array(input);
        MPI_Finalize();
        return 1;
    }

    // allocate memory for the 3d forward and inverse array
    forward = create_3d_array(l, m, n);
    inverse = create_3d_array(l, m, n);
    if (forward == NULL || inverse == NULL) {
        fprintf(stderr, "error: unable to allocate memory for the 'forward' or 'inverse' array.\n");
        free_3d_array(input);
        free_3d_array(twiddles);
        free_3d_array(forward);
        free_3d_array(inverse);
        MPI_Finalize();
        return 1;
    }

    if (rank == 0) {
        printf("running fourier transform on %dx%dx%d problem using %d process(es).\n", l, m, n, size);
        printf("time taken to precompute twiddles: %f seconds.\n", stop - start);
        printf("a small part of the input array 'input':\n");
        print_numbers(input, 3);
    }

    // run the fourier transform forward and inverse, checking correctness
    // perform forward transform
    duration = parallel_run_transform(input, forward, l, m, n, 0, twiddles);
    if (rank == 0) {
        printf("execution time (forward): %f seconds.\n", duration);
        printf("a small part of the output array 'forward':\n");
        print_numbers(forward, 3);
    }

    // perform inverse transform
    duration = parallel_run_transform(forward, inverse, l, m, n, 1, twiddles);
    if (rank == 0) {
        printf("execution time (inverse): %f seconds.\n", duration);
        printf("a small part of the output array 'inverse':\n");
        print_numbers(inverse, 3);

        // check how close 'inverse' is to 'input'
        double error = check_inverse_error(input, inverse, l, m, n);
        printf("relative error after inverse = %e\n", error);
    }

    // free allocated memory
    free_3d_array(input);
    free_3d_array(twiddles);
    free_3d_array(forward);
    free_3d_array(inverse);

    MPI_Finalize();
    return 0;
}

parallel_fourier_transform.c

#include <mpi.h>
#include <math.h>
#include <complex.h>
#include <time.h>
#include <stddef.h>
#include "parallel_fourier_transform.h"
#include "fourier_transform.h"
#include "utils.h"

double parallel_run_transform(double complex ***input, double complex ***output, int l, int m, int n, int inverse, double complex ***twiddles) {
    double start = MPI_Wtime();
    parallel_fourier_transform(input, output, l, m, n, inverse, twiddles);
    double stop = MPI_Wtime();
    return stop - start;
}

void parallel_fourier_transform(double complex ***input, double complex ***tilde, int l, int m, int n, int inverse, double complex ***twiddles) {
    double total = (double) (l * m * n);
    int rank, size;
    MPI_Comm_rank(MPI_COMM_WORLD, &rank);
    MPI_Comm_size(MPI_COMM_WORLD, &size);

    int local_l = l / size;
    int start_index = rank * local_l;

    // if l is not perfectly divisible by size, last process handles the remainder
    if (rank == size - 1) {
        local_l += (l % size);
    }

    // temporary array to hold local results
    double complex ***local_tilde = create_3d_array(local_l, m, n);

    for (int u = 0; u < local_l; u++) {
        for (int v = 0; v < m; v++) {
            transform_index(input, local_tilde[u][v], l, m, n, start_index + u, v, total, inverse, twiddles);
        }
    }

    // gather results from all processes
    MPI_Allgather(local_tilde[0][0], local_l * m * n, MPI_DOUBLE_COMPLEX, tilde[0][0], local_l * m * n, MPI_DOUBLE_COMPLEX, MPI_COMM_WORLD);

    free_3d_array(local_tilde);
}

Strategies for Domain Decomposition and Communication

In the parallel implementation, domain decomposition is achieved by dividing the 3D array along the first dimension $(l)$ and distributing the subarrays among the available processes. Each process handles a subset of the entire array, which reduces the computational load on each process and allows for concurrent execution.

Domain Decomposition:

• The first dimension $(l)$ of the 3D array is divided evenly among the available processes. Each process works on a contiguous block of $\frac{l}{\text{size}}$ slices.
• The function parallel_fourier_transform calculates the start and end indices for each process based on its rank and the total number of processes.

Communication:

• After each process completes its portion of the computation, the results are gathered using MPI_Allgather, which collects the data from all processes and distributes the complete array to each process.
• MPI_Allgather is crucial for ensuring that all processes have the updated and complete results after the parallel computation.

Performance Metrics for the Parallel Implementation

The following performance metrics were recorded during the execution of the FT on a $48 \times 48 \times 48$ problem using six processes:

• Time taken to precompute twiddles: 0.000286 seconds
• Execution time (forward transform): 18.018013 seconds
• Execution time (inverse transform): 20.413443 seconds

These metrics demonstrate the significant reduction in execution time achieved by parallelising the FT. The input and output data snippets provide a brief look at the transformation results, ensuring the correctness of the parallel implementation.

Sample output snippets:

• Input array:

  2 + -2i
  4 + -4i
  6 + -6i

• Forward transform output:

  1.57672e+06 + 1.7979e+06i
  729438 + 950622i
  445392 + 666576i

• Inverse transform output:

  2 + -2i
  4 + -4i
  6 + -6i

These results validate the accuracy and efficiency of the parallel FT implementation using MPI.

Running on ARCHER2 Using SLURM

The next step in this article is to test the serial and parallel versions of our FT example on the ARCHER2 supercomputer. This will allow us to evaluate the performance and scalability of our implementations on a high-performance computing system.

Overview of ARCHER2 Supercomputer

ARCHER2 is the UK’s next-generation national supercomputing service, hosted by the University of Edinburgh. It provides high-performance computing resources to the UK research community, enabling large-scale scientific and engineering simulations. ARCHER2 comprises of 5,860 compute nodes, each equipped with 128 AMD EPYC cores (256 SMT threads) and 256 GB of memory, interconnected by a high-speed Cray Slingshot network. As a student at the University of Edinburgh, I have access to this powerful system, which provides a substantial computational resource for research and development.

Introduction to SLURM Job Scheduler

SLURM (Simple Linux Utility for Resource Management) is an open-source, highly scalable job scheduler used by many of the world’s largest supercomputers, including ARCHER2. It allocates resources, schedules jobs, and manages job queues. SLURM enables users to define their job requirements and submit jobs to the queue, where they are scheduled for execution based on resource availability and priority.

Writing and Submitting SLURM Job Scripts

To run our FT example on ARCHER2, we need to write and submit a SLURM job script. This script specifies the resources required, the executable to run, and any necessary environment setup.

I have run the following scripts on ARCHER2:

srun-strong-scaling.slurm

#!/bin/bash

#SBATCH --job-name=journal.fourier.transform
#SBATCH --time=2:00:00
#SBATCH --exclusive
#SBATCH --nodes=2
#SBATCH --tasks-per-node=128
#SBATCH --cpus-per-task=1
#SBATCH --threads-per-core=1
#SBATCH --account=<your-account>
#SBATCH --partition=standard
#SBATCH --qos=standard
#SBATCH --hint=nomultithread
#SBATCH --distribution=block:block

# load the default hpe mpi environment
module load PrgEnv-gnu
module load cray-mpich/8.1.23

# change to the submission directory
cd $SLURM_SUBMIT_DIR

# set the number of threads to 1
# this prevents any threaded system libraries from automatically using threading.
export OMP_NUM_THREADS=1

# set problem size
l=256
m=32
n=32

mkdir -p ./slurm/srun-$SLURM_JOB_ID/

# logarithmic scaling for processes: 2^0, 2^1, ..., 2^8
# the maximum we can go is (nodes * ntasks-per-node).
for processes in 1 2 4 8 16 32 64 128 256
do
    # if 'processes' exceeds the total hardware cores, we skip.
    # e.g., if processes=128 but we only have 2*128=256 exact tasks, that might be okay.
    if [[ "$processes" -gt $((SLURM_NNODES * SLURM_NTASKS_PER_NODE)) ]]; then
        continue
    fi

    echo "strong scaling: processes=${processes}, l=${l}, m=${m}, n=${n}"

    srun --ntasks=${processes} \
         --cpu-bind=cores \
         ./fourier -l ${l} -m ${m} -n ${n} \
         > "./slurm/srun-${SLURM_JOB_ID}/fourier_${processes}.out" 2>&1
done

# wait for all background jobs to finish
wait

srun-weak-scaling.slurm

#!/bin/bash

#SBATCH --job-name=journal.fourier.transform
#SBATCH --time=2:00:00
#SBATCH --exclusive
#SBATCH --nodes=2
#SBATCH --tasks-per-node=128
#SBATCH --cpus-per-task=1
#SBATCH --threads-per-core=1
#SBATCH --account=<your-account>
#SBATCH --partition=standard
#SBATCH --qos=standard
#SBATCH --hint=nomultithread
#SBATCH --distribution=block:block

# load the default hpe mpi environment
module load PrgEnv-gnu
module load cray-mpich/8.1.23

# change to the submission directory
cd $SLURM_SUBMIT_DIR

# set the number of threads to 1
# this prevents any threaded system libraries from automatically using threading.
export OMP_NUM_THREADS=1

# base problem size
l_base=256
m_base=32
n_base=32

mkdir -p ./slurm/srun-$SLURM_JOB_ID/

# logarithmic scaling for processes: 2^0, 2^1, ..., 2^8
# the maximum we can go is (nodes * ntasks-per-node).
for processes in 1 2 4 8 16 32 64 128 256
do
    # if 'processes' exceeds the total hardware cores, we skip.
    # e.g., if processes=128 but we only have 2*128=256 exact tasks, that might be okay.
    if [[ "$processes" -gt $((SLURM_NNODES * SLURM_NTASKS_PER_NODE)) ]]; then
        continue
    fi

    # each rank keeps about the same sub-domain size => total domain scales ~ processes
    # for a naive approach, let's scale l by processes^(1/3),
    # so total volume ~ processes * base_volume.
    scaling_factor=$(awk "BEGIN {print $processes^(1.0/3.0)}")
    l=$(printf "%.0f" "$(echo "${l_base} * ${scaling_factor}" | bc -l)")
    #m=$(printf "%.0f" "$(echo "${m_base} * ${scaling_factor}" | bc -l)")
    #n=$(printf "%.0f" "$(echo "${n_base} * ${scaling_factor}" | bc -l)")
    m=$m_base
    n=$n_base

    # our code requires l % processes == 0, let's pad l to be divisible by 'processes'
    if [[ ${processes} -gt 1 ]]; then
        remainder=$(( l % processes ))
        if [[ "${remainder}" -ne 0 ]]; then
            l=$(( l + (processes - remainder) ))
        fi
    fi

    echo "weak scaling: processes=${processes}, l=${l}, m=${m}, n=${n}"

    srun --ntasks=${processes} \
         --cpu-bind=cores \
         ./fourier -l ${l} -m ${m} -n ${n} \
         > "./slurm/srun-${SLURM_JOB_ID}/fourier_${processes}.out" 2>&1
done

# wait for all background jobs to finish
wait

In these scripts:

• #SBATCH directives specify the job’s resource requirements and configuration.
• The <your-account> placeholder should be replaced with your specific account information.
• module load commands load the necessary software modules (e.g. GCC and OpenMPI).
• The srun command runs the specified executable (fourier) with different problem sizes and process counts.

Submitting the Jobs

To submit these jobs to the SLURM job scheduler, use the following commands:

sbatch srun-strong-scaling.slurm
sbatch srun-weak-scaling.slurm

Monitoring and Analysing Job Performance

Once the job scripts are submitted using the sbatch command, you can monitor the status and performance of your jobs using SLURM commands:

• Check job status: squeue -u <your-username>
• View job details: scontrol show job <job-id>
• Cancel a job: scancel <job-id>

To analyse the performance of your jobs, you can examine the output and error files specified in the job script (e.g. fourier_1.out, fourier_256.out). These files will contain information about the job’s execution, including any print statements from your program and SLURM-related messages.

For more detailed performance analysis, consider using profiling tools such as perf, gprof, or specialised tools available on ARCHER2, to measure metrics like CPU usage, memory usage, and communication overhead.

By running our FT example on ARCHER2 using SLURM, we can gain valuable insights into the performance and scalability of our serial and parallel implementations, allowing us to optimise our code for high-performance computing environments.

Performance Analysis

Strong Scaling Analysis

Strong scaling analysis measures how efficiently a fixed‐size problem can be solved faster by adding more processors. We examined the parallel performance of our Fourier Transform (FT) implementation on a constant‐size dataset, comparing its execution time when running on 1, 2, 4, …, up to 256 processors.

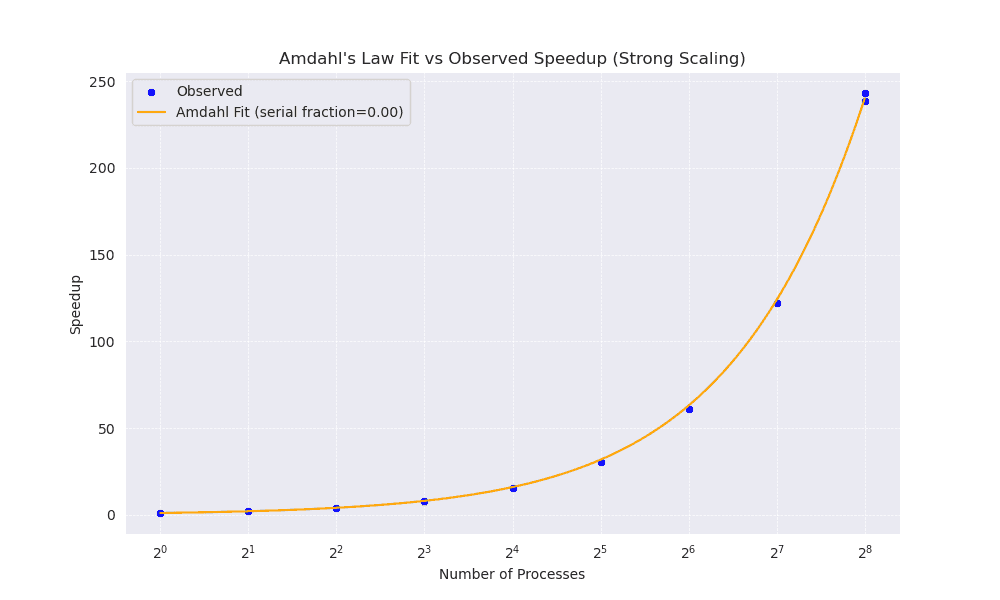
The Amdahl’s Law Fit vs Observed Speedup (Strong Scaling) plot (Figure 1) shows both the empirically measured speedup (blue markers) and the theoretical fit (orange line) derived from Amdahl’s Law with a serial fraction near zero. Amdahl’s Law states:

$\text{Speedup}(p) = \frac{1}{(1 - \alpha) + \frac{\alpha}{p}}$

where:

• $p$ is the number of processors,
• $\alpha$ is the parallel fraction of the code (so $1 - \alpha$ is the serial portion).

Given the near‐zero serial fraction observed (i.e. $\alpha \approx 1.0)$, the speedup curve remains very close to an ideal linear trend, even at higher processor counts. Notably, the speedup reaches 243 when scaling from 1 to 256 processors, implying highly efficient parallelisation.

Figure 1

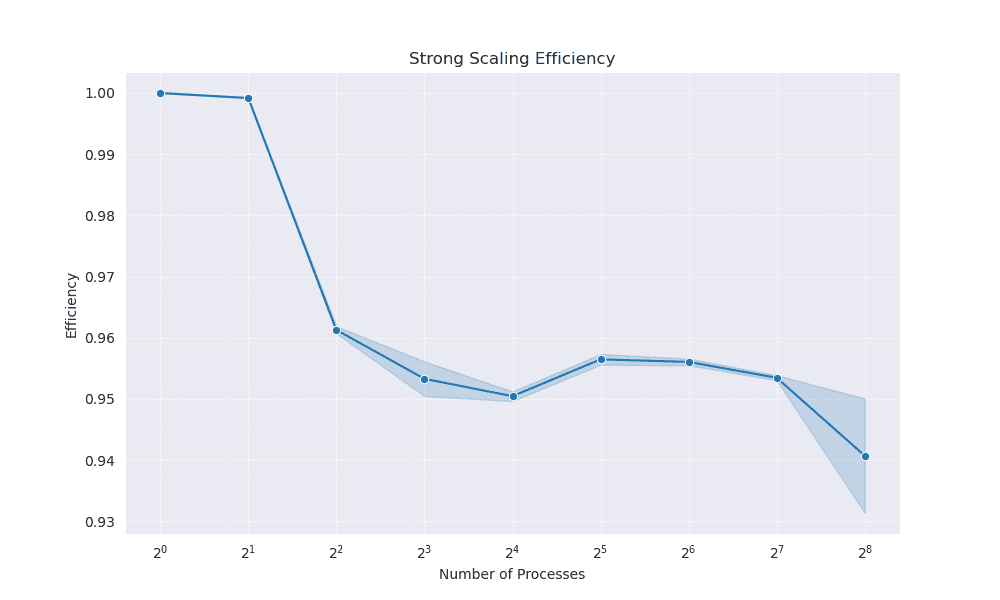
This efficiency is further illustrated by the Strong Scaling Speedup (Figure 2) and Strong Scaling Efficiency (Figure 3) plots. The speedup curve (Figure 2) rises steeply, showing near‐linear scaling up to 256 processors. Meanwhile, the strong scaling efficiency plot (Figure 3) demonstrates only a modest decline from nearly 100% efficiency on a single processor to around 94% efficiency at 256 processors. This indicates that additional processors continue to yield substantial performance benefits, with only minor overheads.

Figure 2

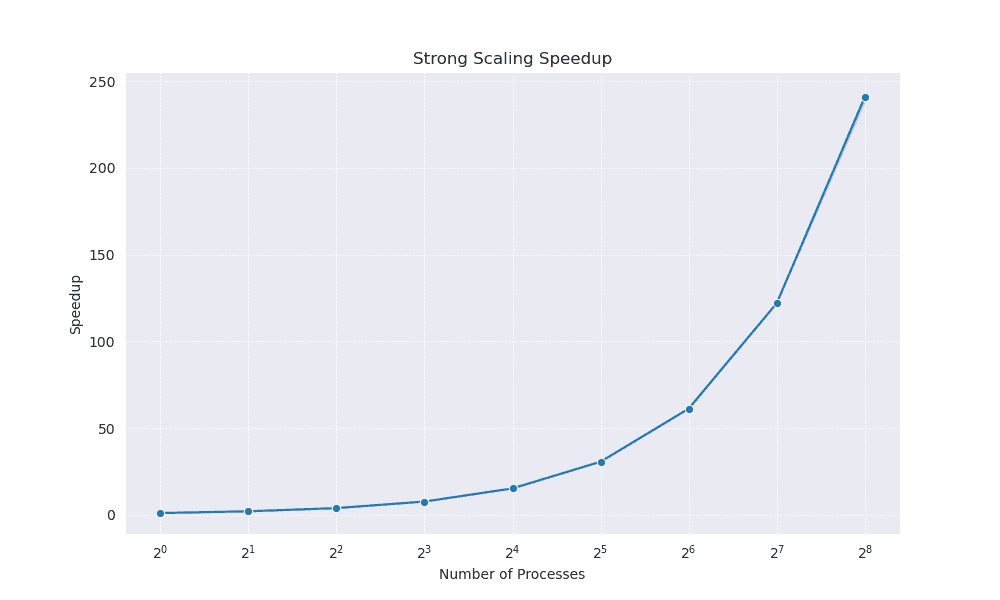
Figure 3

Overall, these results confirm that the parallel implementation exhibits excellent strong scaling. By reducing the serial component to a negligible level, the code capitalises on the compute resources effectively, maintaining high efficiency even as the number of processors grows.

Weak Scaling Analysis

Weak scaling aims to measure how well an application can handle proportionally larger workloads when more processors are added. In other words, each processor maintains roughly the same workload size, and the total problem size grows in step with the number of processors. For our FT code, we tested problem dimensions that increase as the number of processes does so that each process handles a similar number of grid points.

Execution Time and Comparison of Forward vs Inverse Transforms

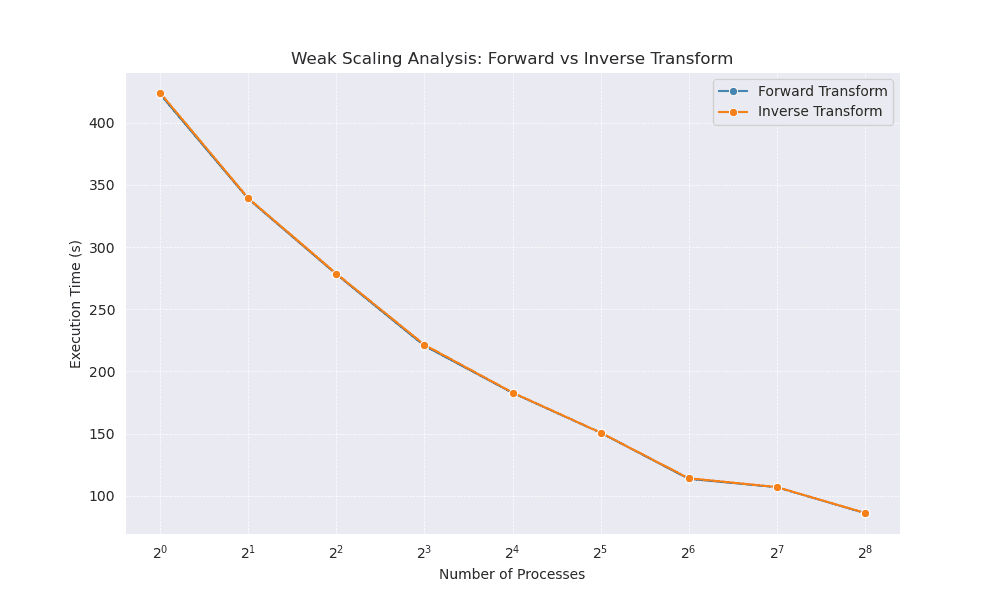
The Weak Scaling Analysis for Forward vs Inverse Transform (Figure 4) shows how the execution time varies with the number of processors for both the forward and inverse versions of the transform. As more processors become available and the grid size grows, the following trends are evident:

1. Overall Decrease in Execution Time: Up to around 256 processes, the per‐processor workload remains nearly constant, and the total execution time decreases to about 100 s.
2. Slight Differences Between Forward and Inverse Transforms: The forward and inverse transform exhibit similar behaviour. Slight variations in runtime may be attributed to differences in how data are accessed and accumulated during the inverse operation versus the forward operation.

Figure 4

The relatively consistent downward slope in the runtime indicates that the code sustains some degree of weak scaling efficiency; however, true perfect weak scaling (constant total runtime as problem size and processor count grow) is rarely observed in practice.

Gustafson’s Law Fit vs Observed Speedup

Gustafson’s Law provides a model for weak scaling. It states that, if the majority of the workload is parallelisable, then larger problems can be solved in roughly the same amount of time by increasing the number of processors, with speedup defined by:

$\text{Speedup}(p) = p - (1 - \alpha)(p - 1)$

where:

• $p$ is the number of processors,
• $\alpha$ is the parallel fraction of the code (so $1 - \alpha$ is the serial component).

The Gustafson’s Law Fit vs Observed Speedup (Weak Scaling) graph (Figure 5) illustrates the observed speedup (blue markers) versus the Gustafson fit (orange line). Here, a serial fraction of 0.98 (i.e. $\alpha = 0.02)$ suggests that although a large proportion of the code is parallelisable, a small part remains strictly serial. Key observations include:

1. Sub‐Ideal Speedup: As the number of processors increases, the observed speedup grows but does not perfectly match the theoretical curve.
2. Impact of Serial Fraction: Even a 2% serial portion can lead to noticeable performance degradation at high concurrency.
3. Communication and Synchronisation Overheads: These factors also contribute to the deviation from Gustafson’s Law, as increasing processor count often increases interprocess data transfer and coordination costs.

Figure 5

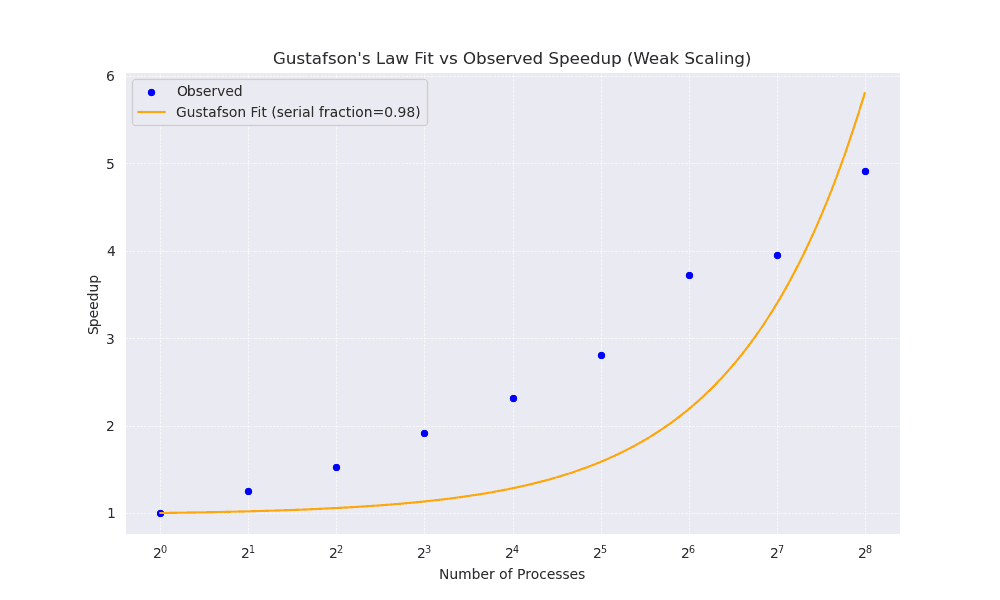
Overall, these weak scaling results suggest that the code can handle larger problem sizes on more processors to a point, but serial overheads, communication burdens, and load imbalance prevent achieving near‐ideal speedup. Nonetheless, the code demonstrates a viable scaling strategy for moderate problem sizes, especially when distributed over dozens or even hundreds of processes.

Discussion

Strong Scaling

The revised strong scaling results underscore the importance of minimising serial work for achieving high performance on many processors. Amdahl’s Law aptly demonstrates that when the serial fraction is nearly zero, the overall speedup grows close to linearly with increasing processor count. Thus, the code’s parallel fraction appears to be exceptionally large, meaning that the majority of the computation can be split across multiple processors.

Comparison with Theoretical Predictions

The observed data align closely with Amdahl’s Law under the assumption of a negligible serial fraction. Whilst many parallel applications exhibit a clear limit to scalability (due to non‐parallelisable sections of the algorithm), the FT implementation here shows that it is possible to approach near‐ideal strong scaling. Minor deviations from the perfect linear speedup can be attributed mainly to communication overhead and synchronisation among processors rather than any significant serial workload.

Factors Affecting Scaling Efficiency

Given the near‐ideal scaling, the small losses in efficiency at higher processor counts are most likely attributed to:

• Communication overhead: Data exchange between processors inevitably grows with process count, though it remains relatively small here.
• Synchronisation costs: Barrier synchronisations, collective operations, or global communication steps can slightly reduce efficiency.
• System architecture: Memory bandwidth and interconnect speeds may start to limit throughput at higher concurrency levels, though the impact in this work is clearly minor.

Weak Scaling

Unlike strong scaling—where the focus is on accelerating a fixed problem size—weak scaling assesses the ability to maintain a similar per‐processor workload while scaling up the total problem dimension. Although the observed data follow Gustafson’s Law reasonably well initially, increased overheads and a finite serial fraction cause discrepancies at higher concurrency.

Comparison Between Gustafson’s Law Prediction and Actual Performance

In principle, a small serial fraction $(\alpha \approx 0.98)$ should yield significant gains as the system grows. However, the experimental curves diverge from the ideal primarily due to:

• Communication Costs: Increasing the number of processes often requires more frequent and/or larger data exchanges.
• Load Imbalance: Especially when the domain partitioning is imperfect.
• Memory and Interconnect Limits: Real‐world hardware introduces bandwidth constraints and latencies not accounted for by the ideal model.

Factors Affecting Weak Scaling Efficiency

• Serial Routines: Even if they account for 2% of the runtime, they become disproportionately influential at high processor counts.
• Communications Overhead: Inter‐processor synchronisation times can grow significantly with more processes.
• Domain Partitioning: Effective domain decomposition is crucial for minimising waiting times and idle processors.

Conclusion

Strong Scaling

1. Near‐ideal Strong Scaling: The graphs reveal that the FT implementation achieves excellent scaling from 1 to 256 processors, with speedups approaching 250 at the highest concurrency levels.
2. Negligible Serial Fraction: Amdahl’s Law analysis indicates a serial component of almost zero, allowing near‐linear speedup.
3. Sustained High Efficiency: Efficiency remains close to 100% for lower processor counts and above 90% at 256 processors, reflecting minimal overheads.

Weak Scaling

1. Moderate Adherence to Gustafson’s Law: The parallel fraction is high $(\alpha \approx 0.98)$, resulting in a reasonable but not ideal speedup for large‐scale runs.
2. Execution Time Decreases with Processor Count: The time for the forward and inverse transforms both drop significantly as more processes tackle a proportionally larger workload.
3. Overheads Limit Scalability: A small serial fraction and non‐trivial communication overheads prevent the code from reaching perfect linear speedup under weak scaling.

Disclaimer

It should be noted that the triple loop in transform_index() implements a direct Fourier Transform, with a computational complexity of $\mathcal{O}(n^4)$ for a three‐dimensional domain of size $n \times n \times n$. This approach does not constitute a Fast Fourier Transform (FFT). For large‐scale high‐performance computing, adopting a more efficient scheme, such as the Cooley–Tukey algorithm⁸, or utilising an established parallel FFT library (e.g. MPI‐FFTW) would be advisable. Nevertheless, for illustrative purposes or small‐scale educational code, the single‐block allocation method described herein can mitigate segmentation faults and enhance code reliability.